|
19.07.2014, 21:32
 Beitrag #1 Beitrag #1 |
|
|
|
|
|
20.07.2014, 07:33
 Beitrag #2 Beitrag #2 |

cb

LVF-SeniorMod
Beiträge: 1.731
Registriert seit: Feb 2006
2018SP1
2001
EN
40xxx
Deutschland
|
RE: Phasenspektrum
der Grund dafür ist, dass Double-Werte zwar schon recht vieeeeeeeele Nachkommastellen haben, es aber immer noch diskrete Werte sind. Das kleinste Inkrement zwischen zwei Fielßkommazahlnen heist "Epsilon", und man könnte das auch als so eine Art Rundungsfehler bezeichnen.
Wenn man nun die beiden Signale vergleicht (S1 minus S2) und das ganze mit dem Bezugswert "Epsilon" in einer dB-Skala darstellt, sieht man dass da sehr wohl Unterschiede zwischen den beiden Signalen vorhanden sind, die sich dann eben so auswirken, dass das Phasen-Spektrum nicht gleich aussieht ...
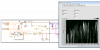
|
|
|
|
20.07.2014, 08:49
(Dieser Beitrag wurde zuletzt bearbeitet: 20.07.2014 08:50 von Lucki.)
 Beitrag #3 Beitrag #3 |

Lucki

Tech.Exp.2.Klasse

Beiträge: 7.699
Registriert seit: Mar 2006
LV 2016-18 prof.
1995
DE
01108
Deutschland
|
RE: Phasenspektrum
Hier hate ich das schon mal erklärt - mit Beispiel.
Da mußtest Du ja über Deinen eigenen (Namens-)Schatten springen: Hast richtigerweise bei der Fourier-Transformation des "Rechteck" - Fenster gewählt, und nicht das "Hamming"-Fenster. 
|
|
|
|
|
20.07.2014, 09:41
 Beitrag #4 Beitrag #4 |
Hamming

LVF-Neueinsteiger
Beiträge: 4
Registriert seit: Jul 2014
2012 Student Edition
2012
DE
|
RE: Phasenspektrum
Vielen Dank für die Antworten.
Ich hatte schon vermutet, dass die Ursache in den Nachkommastellen steckt. Aber da die Phasenspektren so unterschiedlich aussahen, war ich mir doch unsicher.
Das Problem müsste daran liegen, dass der arctan() für die Phase gebildet wird und deshalb die kleinen Amplitudenwerte so groß werden.
Nochmals herzlichen Dank.
Hamming
|
|
|
|
20.07.2014, 19:45
(Dieser Beitrag wurde zuletzt bearbeitet: 20.07.2014 19:47 von Lucki.)
 Beitrag #5 Beitrag #5 |

Lucki

Tech.Exp.2.Klasse

Beiträge: 7.699
Registriert seit: Mar 2006
LV 2016-18 prof.
1995
DE
01108
Deutschland
|
RE: Phasenspektrum
(20.07.2014 09:41 )Hamming schrieb: Das Problem müsste daran liegen, dass der arctan() für die Phase gebildet wird und deshalb die kleinen Amplitudenwerte so groß werden.
Formulierung gefällt mit nicht. Vielleicht so:
Wenn die Amplitude gegen Null geht, dann geht die Phase gegen Unbetimmt (sie ist weder Null noch etwas anderes) :
Phi = arctan(Im/Re) --> arctan(0/0) = arctan(NaN) = NaN = unbestimmt
|
|
|
|
|
20.07.2014, 19:58
 Beitrag #6 Beitrag #6 |
Hamming

LVF-Neueinsteiger
Beiträge: 4
Registriert seit: Jul 2014
2012 Student Edition
2012
DE
|
RE: Phasenspektrum
Ist es aber dann nicht so, dass ich für NaN eigentlich keine Phasenwerte erhalten dürfte?
Da ich aber dennoch Phasenwerte erhalte, sind Im und Re ungleich 0, sondern nur sehr sehr keine Werte.
So habe ich das verstanden, oder liegt bei mir ein Denkfehler vor?
|
|
|
|
21.07.2014, 08:52
(Dieser Beitrag wurde zuletzt bearbeitet: 21.07.2014 08:58 von Lucki.)
 Beitrag #7 Beitrag #7 |

Lucki

Tech.Exp.2.Klasse

Beiträge: 7.699
Registriert seit: Mar 2006
LV 2016-18 prof.
1995
DE
01108
Deutschland
|
RE: Phasenspektrum
(20.07.2014 19:58 )Hamming schrieb: Ist es aber dann nicht so, dass ich für NaN eigentlich keine Phasenwerte erhalten dürfte?
Da ich aber dennoch Phasenwerte erhalte, sind Im und Re ungleich 0, sondern nur sehr sehr keine Werte.
So habe ich das verstanden, oder liegt bei mir ein Denkfehler vor?
Mein Denkfehler war, dass ich davon ausging, das wäre alles durch die vorangegangenen Beiträge von Cb und mir schon geklärt gewesen. Es wurde ja schon gesagt, das wegen des Qantisierungsrauschens Real-und Imaginärteil nie Null sind, und bei der Phasenberechnung kommt dann irgendeinen Zahl heraus, die aber irrelevant ist und "eigentlich" NaN sein müsste. Soweit klar. Dann aber kamst Du nochmal und schriebst, dass dann " die kleinen Amplitudenwerte so groß werden" (Sicher meinst Du heir die "Phasenwerte") . Es kann natürlich sein, dass bei Division zweier sehr kleiner zufälliger Zahlen ein großes Ergebnis herauskommt. Aber das ist dann auch zufällig und bedeutungslos.
Man sollte jedenfalls die Phasen extrem kleiner Amplituden im Spektrum am besten in einer gesonderten Prozedur auf "NaN" setzen. In verlinkten Beispiel hatte ich das gemacht.
|


|
|
|
|
21.07.2014, 15:29
 Beitrag #8 Beitrag #8 |
Hamming

LVF-Neueinsteiger
Beiträge: 4
Registriert seit: Jul 2014
2012 Student Edition
2012
DE
|
RE: Phasenspektrum
Sehr gut, dann sind wir uns ja einig. :-)
Eine Sache ist mir aber noch unklar:
Nach Recherchen fasse ich das Epsilon als einen Parameter des Rechners auf. Spielt dieser bei der Verwendung von Double überhaupt eine Rolle?
Ensteht nicht der Fehler durch Operationen mit den Double-Werten alleine?
Vielleicht ist die Frage hier etwas Fehl am Platz, aber wenn wir schon dabei sind!?
Vielen Dank für die übrigen Antworten.
|
|
|
|
|
21.07.2014, 15:55
 Beitrag #9 Beitrag #9 |

GerdW

______________

Beiträge: 17.465
Registriert seit: May 2009
LV2021
1995
DE_EN
10×××
Deutschland
|
RE: Phasenspektrum
Hallo Hamming,
Zitat:Spielt dieser bei der Verwendung von Double überhaupt eine Rolle?
Ensteht nicht der Fehler durch Operationen mit den Double-Werten alleine?
Epsilon spielt eine Rolle, und man sollte als Programmierer halbwegs darüber informiert sein.
Siehe Links in meiner Signatur…
|
|
|
|
21.07.2014, 16:12
(Dieser Beitrag wurde zuletzt bearbeitet: 21.07.2014 16:39 von Lucki.)
|

Lucki

Tech.Exp.2.Klasse

Beiträge: 7.699
Registriert seit: Mar 2006
LV 2016-18 prof.
1995
DE
01108
Deutschland
|
RE: Phasenspektrum
(21.07.2014 15:29 )Hamming schrieb: Entsteht nicht der Fehler durch Operationen mit den Double-Werten alleine?
Genau so ist es, die Bezeichnung "Maschinengenauigkeit" ist historisch bedingt und hat ihre eigentliche Berechtigung dort, wo die Gleitkommaberechnungen in einem Hardware - Gleitkommaprozessor mit feststehender Genauigkeit ausgeführt werden *). Zu den in Labview benutzten Gleitkommaformaten SGL, DBL und Ext gehören übrigens unterschiedliche Epsilons, auswählbar über Kontextmenü.
Allles Weitere siehe Wikipedia.
*) Man könnte aber auch sagen, die Bezeichnung ist korrekt, denn die Tatsache, das es nicht einfach die "Gleitkommazahl" als solche gibt, sondern die verschiedenen Formate derselben, hängt ja mit der immer begrenzten Rechenfähigkeit des Computers zusammen.
|
|
|
|
| |