Inverse FFT, kein konstantes df

Hallo!

Ich möchte die inverse FFT machen, jedoch bekomm ich da nur Murks raus ;-)
Ich habe ein Bode-Diagramm, also Betragsspektrum und Phasenspektrum. Das df ist bei mir jedoch nicht konstant, z.B. bei der Resonanzstelle ist es viel kleiner, wie in anderen Bereichen.
Wie kann das VI "Inverse FFT" denn wissen, zu welchen Frequenzen, die einzelnen Amplituden bzw. Phasen gehören? Muss ich vorher auch das Spektrum spiegeln, wie es beim Ergebnis des VI "FFT" der Fall ist?

Das Ziel ist übrigens, aus dem Bode-Diagramm, welches experimentell aufgnommen wurde, durch die IFFT die Impulsantwort zu bekommen.

Wäre super, wenn ihr mir weiterhelfen könntet :-)

viele Grüße
Eric

hier wären Beispieldaten zum Spielen hilfreich
..man könnte die Ausgangssignale nachabtasten

Für die FFT und invers brauchst Du ein ein kontantes dt bzw. df, möglichst von der Anzahl 2^N. Wenn das Bode-Diagramm das nicht hat, dann sollten diese Daten, so wie ImExPorty das schon erwähnt hat, erst einmal neu abgetastet werden. Dafür gibt es VIs. Aus Deinen originalen Daten entsteht dann durch Interpolation ein neuer Datensatz mit konstantem df und der gewünschten Anzahl von Samples.
-- Und wenn Du nicht weiß, wie man Beispieldaten schickt:
Beim VI mit dem Bodediagramm "Menüleiste/Bearbeiten/Aktuelle Werte als Standard" anklicken, alles andere aus dem VI meinetwegen herauslöschen, abpeichern und posten.

Zuerst, danke schonmal für eure Hilfe!

Das Vi "Ausrichten und Neuabtasten" wäre doch dann dies, was ich benötige, oder?
Aber wenn ich das Bodediagramm mit konstantem df abtaste, woher weiß die IFFT, dieses df und das f0? Denn solche Eingänge sind ja nicht vorhanden.
Zum Neuabtasten habe ich noch eine FRage, denn ich habe bisher nur mein Array mit den Betragswerten, ein Array mit den Phasen und eine Array mit den Frequenzen. Das VI "Ausrichten und Neuabstaten" möchte als Eingang jedoch ein Signal. Wie kann ich dies aus den Arrays erzeugen? Mit konstantem df oder dt ist das klar, aber wie mach ich das in diesem Fall?

Habe auch die Daten hochgeladen:

  identi.vi (Größe: 101,07 KB / Downloads: 289)



Gruß
Eric

' schrieb:Das Vi "Ausrichten und Neuabtasten" wäre doch dann dies, was ich benötige, oder?
Aber wenn ich das Bodediagramm mit konstantem df abtaste, woher weiß die IFFT, dieses df und das f0?

Das ifft muß df nicht wissen, das geht dann nur in die Skalierung dt der Zeitfunktion ein:
dt = 1/maximale Frequenz 1((df*Anzahl Samples) (Bei Dir 15 Hz)

Anbei eine kleine Demo, wie es in etwa geht.

   


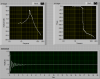
  identi.vi (Größe: 17,37 KB / Downloads: 301)


Ja, und nun möchtest Du wohl noch die Koeffizienten des Laplace-Polynoms wissen welches dieses Verhalten man besten approximiert?

Vielen vielen Dank! :-) Denn das sieht doch super aus!

Am besten schreibe ich mal kurz was zum Hintergrund:
Ein Teil meiner Studienarbeit ist die Identifikation meiner Regelstrecke. Es handelt sich dabei um einen Motor, der Welle antreibt. Die Welle schaut ca. 30 cm aus dem Motor heraus. An dessen Ende ist eine Masse (Scheibe) montiert. Weiterhin ist es möglich verschiedene Drehfedern in die Welle einzuspannen, um ein unterschiedliches dynamisches Verhalten zu erlangen.
Ich hab dies als ein Zweimassenschwinger modelliert und hatte ein System 4.Ordnung erhalten plus ein PT1-Glied für das Motorverhalten (also insgesamt 5.Ordnung)
Da die Eingangsgröße das Drehmoment ist und die Ausgangsgröße die Drehwinkelposition der Scheibe, ist dieses System instabil. Somit ist auch eine Identifikation schwer möglich. Daher habe ich die Strecke mit einem PD-Regler stabilisiert.
Somit steht nun die Identifikation des geschlossenen Regelkreises an. Dieser müsste somit rechnerisch 1 Nullstelle und 6 Pole haben.

Daher möchte ich, wie du gesehen hast, die Laplace-Übertragungsfunktion bestimmen. Aus zwei Gründen: Erstens für weitere Reglerentwürfe (Iterativ lernende Regelung) und zweitens, um die Parameter der Regelstrecke zu bestimmen.
Seh ich das richtig, dass dies hier aber nicht möglich ist? Zumindest nicht mit den Zähler- und Nennerordnungen wie ich es berechnet habe? Denn dann hätte ich nicht mehr das Verhalten, wie es das Bode-Diagramm darstellt.
Ich vermute, dass es daran liegt, dass sich die anderen Pole erst bei höheren Frequenzen bemerkbar machen. Jedoch ist unsere Abtastfrequenz aller Signale stets 100 Hz, somit kann ich diese Pole auf Grund des Nyquist-Theorems ja nie zum Vorschein bringen.
Heißt das also, dass ich mit Hilfe meines Bode-Diagramms, nur auf ein PT2-Glied (Resonanz, Phasenabfall 180 Grad) kommen kann und eine Parameterschätzung daher nicht möglich ist?

Ui, jetzt hab ich aber ganz schön viel geschrieben ;-) Ich hoffe, dass es trotzdem einigermaßen verständlich ist :-)

viele Grüße
Eric

Hallo!

Mir ist grad noch etwas aufgefallen. Bist du dir sicher, dass die Skalierung der Y-Achse richtig ist? Denn das Ergebnis einer FFT ist ja skaliert. Wenn ich diese Skalierung rausrechne und daraus, die Inverse FFT mache, bekomme ich nicht das ursprüngliche Signal. Somit müsste man doch vor bzw. nach der Inversen FFT eine Skalierung machen, oder?


GRuß
Eric

' schrieb:Ein Teil meiner Studienarbeit ist die Identifikation meiner Regelstrecke. Es handelt sich dabei um einen Motor, der Welle antreibt. Die Welle schaut ca. 30 cm aus dem Motor heraus. An dessen Ende ist eine Masse (Scheibe) montiert. Weiterhin ist es möglich verschiedene Drehfedern in die Welle einzuspannen, um ein unterschiedliches dynamisches Verhalten zu erlangen.
Ich hab dies als ein Zweimassenschwinger modelliert und hatte ein System 4.Ordnung erhalten plus ein PT1-Glied für das Motorverhalten (also insgesamt 5.Ordnung)

Sowie Du es beschreibst ist es doch ein einfaches Masse-Federsystem mit Übertragungfunktion 2. Ordnung, und mehr läßt sich auch aus dem Plot nicht herauslesen. Natürlich ist es in Wirklichkeit ein System mit verteilten Parametern, und bei höheren Frequenzen gibt es zusätzlich jede Menge Partialresonanzen, die den Entwickler eines Regelsystems zur Verzweiflung bringen können.


  Filter.vi (Größe: 32,83 KB / Downloads: 260)

' schrieb:Mir ist grad noch etwas aufgefallen. Bist du dir sicher, dass die Skalierung der Y-Achse richtig ist?

Daß sie nicht ganz falsch sein kann, sieht man doch sofort: Im Bode-Plot gibt es eine Resonanz bei 3 Hz, und dementsprechend gibt es im berechneten Zeitverlauf eine abklingende Schwingung von 3Hz.

Ja die Skalierung der x-Achse ist richtig, da wie du auch meintest, die Resonanzfrequenz erkennbar ist.
Aber ich meinte die y-Achse.
Denn aus dem Bodediagramm, ist zu erkennen, dass im Resonanzfall der Betragswert 6 ist, bzw. 15 dB.
Jedoch sind die Amplituden vom Ergebnis der IFFT viel kleiner als 6.
Wie kann das sein?

Welche Skalierungen muss ich denn bei der FFT und IFFT beachten?
Bei der IFFT muss ich die Zeitachse skalieren, in der Art und Weise, wie du es oben erläutert hast.
Und bei der FFT muss man ja das Ergebnis durch die Hälfte der Eingangsarraygröße dividieren.
Gibt es sonst noch was zu beachten?

Gruß
Eric

Normalerweise nerve ich ja nicht so gerne ;-) Aber muss doch nochmal um Hilfe bitten, da ich deswegen bei meiner Studienarbeit hänge.

viele Grüße
Eric