Aufrunden bis zum nächsten Vielfachen

Hallo,

ich habe einen Wert, beispielsweise 300, und möchte nun bis zum nächsten Vielfachen von 16 runden.
Gibt es eine Funktion die das kann? Und wenn ja, wie heisst die?
Denn bis jetzt habe ich nur gefunden, wie man bis zur nächsten ganzen Zahl auf oder abrunden kann...

Danke!

Mir ist jetz zwar nicht mal bekannt, dass es sowas mit abrunden gibt, aber nach dem was ich weiß gibt es nur die Gaußklammern für ganzzaliegs Runden. (Palette: Mathematik -> Numerisch)

So wäre eine Umsetzung. Die macht bei 16 eine 32 als Ausgabe, wenn das nicht sein soll kann man den Rest in eine Case führen und auf 0 prüfen.
   
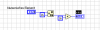
Wobei mir beim schreiben grad noch ein Fehler aufällt^^
Aus der Addition muss eine Multiplikation werden.

Juhuuuu,
ich weiss auch mal was!

Round To -Infinity
Truncates the input to the next lowest integer.

... dann ist also mal wieder selber ausrechnen angesagt...

' schrieb:Round To -Infinity
Truncates the input to the next lowest integer.

Die Funktion ist die untere Gaußklammer und rundet bis zur nächstkleineren ganzen Zahl. Da kannst du nicht vorgeben welchen Teiler die Funktion hat.

5,4 = 5
6,4 = 6
5 = 5
etc

' schrieb:... dann ist also mal wieder selber ausrechnen angesagt...

Das selbst rechnen beschränkt sich hier ja nun wirklich auf die simpelste Mathematik. Entweder du nimmst die OriginalZahl, teilst sie durch 16, rundest auf den nächsten Ganzzahligen wert und multiplizierst wieder mit 16 oder du nimmst die modulo funktion und addierst einen drauf anstelle der division und dem runden.
   
LG
Torsten

' schrieb:Juhuuuu,
ich weiss auch mal was!

Round To -Infinity
Truncates the input to the next lowest integer.

Wollte damit nur sagen, dass es eine Abrunden Funktion gibt....
Das das nicht die ist, die ich suchte war mir schon klar...

Vielen lieben Dank euch beiden für die Beispielprogramme!!!

Denn selber denken könnte ja klug machen..

Hi,

Du kannst auch die Zahl mit der Binärzahl 11110000 verunden (hier im Beispiel mit 8bit Eingang, sonst entsprechend mehr Einsen vorne dran stellen), damit rundest Du dann entsprechend auf das nächste Vielfache von 16 ab. Wenn Du ab und aufrunden willst, musst du dann den entfernten Teil (wahrscheinlich am besten per Verundung mit 00001111, Größer/kleiner-Vergleich mit 1000 und dann Case-Struktur mit +16 oder halt nicht).

Grüße,

ch

' schrieb:Hi,

Du kannst auch die Zahl mit der Binärzahl 11110000 verunden (hier im Beispiel mit 8bit Eingang, sonst entsprechend mehr Einsen vorne dran stellen), damit rundest Du dann entsprechend auf das nächste Vielfache von 16 ab. Wenn Du ab und aufrunden willst, musst du dann den entfernten Teil (wahrscheinlich am besten per Verundung mit 00001111, Größer/kleiner-Vergleich mit 1000 und dann Case-Struktur mit +16 oder halt nicht).

Grüße,

ch

Das ist wahrscheinlich der schnellste Weg, aber mir wars zu kompliziert das zu erklären *zwinker*.

Heyyyyyy,

Danke!!!!
Schon wieder was dazugelernt!

lg